Just before X'mas, we have a discussion in PGDE class on learning about ratios in similar 3D figures. Apart from computational practice on pure geometric figures, there should be realistic contexts where intuitive consideration of ratios in different dimensions naturally arise. It makes me think of the festive formulas recently encountered in Treegonometry, the math for X'mas tree decoration. This set of formulas is derived by students from the University of Sheffield.
It's interesting to me that the number of baubles does not seem to vary with the surface area of the tree. A quick search on web shows a few critical reviews including comments along this line.
- Christmas Tree Calculations and Math Illiteracy
- Is There a Formula for The 'Perfect' Christmas Tree?
- Deck the halls with tau of holly, formula-la-laaa!

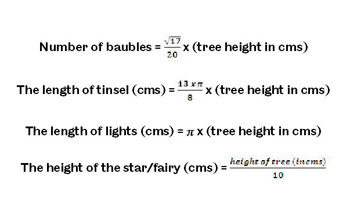
 RSS Feed
RSS Feed
